Антуан Курно народився 28 серпня 1801 року у маленькому бургундському містечку Гре (у Східній Франції) у сім’ї провінційного буржуа. Помітною постаттю у родині Курно був дід Антуана. Він був людиною чесною і принциповою, мав вищу юридичну освіту, працював нотаріусом, користувався незаперечним авторитетом як у сім’ї, так і у мешканців міста. Саме дід наполягав на тому, щоб усі члени родини Курно мали вищу освіту. Він взяв під свою опіку і маленького Антуана. Хлопчик ріс скромною і слухняною дитиною, любив читати, мав багато друзів, але дуже соромився своєї короткозорості. До п'ятнадцяти років він успішно навчався у місцевій школі. Потім продовжив навчання у коледжі міста Безансон та вдома з вчителями-репетиторами, які готували юнака до вступу у вищий навчальний заклад.
У 1821 році Антуан Курно успішно склав іспити і став студентом природничого відділення Вищої нормальної школи (École Normale Supérieure) у Парижі. Вчився він блискуче, захоплювався математикою і вже через два роки отримав своє перше наукове звання – ліценціат (перший учений ступінь у деяких закордонних університетах) у галузі науки. Молодий науковець хотів продовжити навчання, та у Парижі почалися антироялістські заворушення, в яких активну участь брали студенти. Антуан у політичних баталіях участі не приймав – його перш за все цікавила наука. Проте учні Вищої школи брали участь в акціях протесту, уряд її закрив, а всіх студентів, у тому числі і Курно, поліція взяла на облік.
У період з 1823 по 1833 рік Антуан жив у домі маршала Сен-Сіра, де працював його секретарем, домашнім вчителем і вихователем сина. Всі ці роки Курно активно займався науковою діяльністю, відвідував лекції у різних навчальних закладах, опублікував декілька статей. У 1823 році він отримав наукове звання ліценціата у галузі науки, а у 1827 р. – у галузі права, у 1829 році захистив докторську дисертацію з математики у Паризькому університеті, а у 1831 році влаштувався на роботу помічником інспектора Паризької академії. Коло знайомих Курно у цей період складали відомі французькі науковці. Але найбільше він цінував дружбу з видатним вченим, пером Франції, бароном Сімеоном Пуассоном, який вважав Антуана своїм талановитим учнем.
Завдячуючи протекції Пуассона, молодий доктор наук у 1834 році отримав місце професора математики у Ліонському університеті. Через рік йому запропонували очолити престижну в Європі академію (університет) у Греноблі. На цих посадах Курно проявив себе як здібний організатор наукової роботи, неодноразово отримуючи схвальні відгуки від столичних урядових чиновників. Тому цілком логічно у 1838 році йому довірили більш високу посаду генерального інспектора навчальних закладів Франції. Оскільки політичною діяльністю вчений не займався, вболіваючи тільки за якість навчання, при різних урядах йому роботи вистачало. Так, у період Другої республіки Курно входив до складу урядової комісії з вищої освіти (1848–1851 рр.), при Другій імперії – був членом імперської ради з народної освіти (1851–1854 рр.).
У 1854 році Курно переїхав до міста Діжон, де вісім років працював ректором місцевого університету.
У 1862 році Курно пішов у відставку і оселився у Парижі. З математичною педантичністю він планував свій час, складав розпорядок на день, тиждень, місяць і, намагаючись не порушувати його ні на хвилину, виконував намічену програму. У першій половині дня він переважно займався науковою роботою, а другу присвячував побутовим справам і дозвіллю. Ззовні вчений здавався людиною суворою і непідступною, та заговоривши з ним, люди завжди відзначали не аби яке почуття гумору. Помер Антуан Курно 31 березня 1877 року у своїй паризькій квартирі.
Вчений залишив після себе велику наукову спадщину. Світове визнання здобули його наукові праці з математики «Елементарний трактат з теорії функцій і обчислення нескінченно малих величин» («Traite elementaire de la theorie des fonction et du calcul infinitesimal», 1841 р.), «Про походження і межі схожості між алгеброю і геометрією» («De l’origine et des limites de la correspondence entre l’algebre et la geometrie», 1847 р.); з теорії ймовірностей – «Основи теорії шансів і ймовірностей» («Exposition de la theorie des chances et des probabilites», 1843 р.); з філософії та історії – «Роздуми про рух ідей і подій у Новий час» («Consideration sur la marche des idees et des evenements dans les temps modernes», 1872 р.), «Матеріалізм, віталізм, раціоналізм» («Materialisme, vitalisme, rationalisme», 1875 р.), «Досвід про основи нашого знання і про особливості філософської критики» («Essai sur les fondements de nos connaissances et sur les caracteres de la critique philosophique», 1851 р.), «Викладення послідовного розвитку фундаментальних ідей у природничих науках і в історії» («Traite de l’enchainement des idees fondamentales dans les sciences et dans l’histoire», 1871 р.) та багато інших.
Крім того, Курно був чудовим педагогом. Його перу належать підручник з математики, нарис про установи державної освіти у Франції. Відомий французький математик Бертран, сучасник Курно, писав про нього: «Выдающийся ученый, искусный писатель, ум оригинальный и высокий (élevé) в дедуктивных построениях, Курно был учителем» (Цит. за: Четвериков Н. С. Ог. Курно и его вклад в теорию вероятностей / Н. С. Четвериков // Статистические исследования : (теория и практика) / Н. С. Четвериков ; [ред.-сост. М. Б. Немчинова] ; АН СССР, Центр. экон.-мат. ин-т. – Москва : Наука, 1975. – С. 342). Леон Вальрас також вважав для себе за честь бути його учнем. Курно також є автором цікавих мемуарів з математики, перекладачем або редактором ряду фундаментальних наукових творів, зокрема, двотомного зібрання листів Ейлера (Letteres d’Euler), трактата Гершеля з астрономії та інших. «Таким образом, перед нами во весь рост возвышается фигура французского энциклопедиста XIX в., по глубине знаний, по широкому диапазону интересов, по независимости мысли стоявшего в одном ряду с великими французскими энциклопедистами XVIII в. Его биограф Луи Лиар пишет о нем: «В течение более сорока лет Курно поставил на службу философии глубокие знания математика, энциклопедические познания, проницательность (pénétration) необычных методов анализа, выдающиеся качества изобретателя, и редкую независимость мысли»» (Цит. за: Четвериков Н. С. Ог. Курно и его вклад в теорию вероятностей / Н. С. Четвериков. – С. 342).
Головним економічним твором Курно стали «Дослідження математичних принципів теорії багатства» («Recherches sur les principes mathematiques de la theorie des richesses», 1838 р.). Після виходу друком ця книга довгий час залишалася майже непоміченою. Вона не привернула уваги не тільки широкого загалу читачів, а й професійних економістів. Курно, вважаючи, що причиною цього є складність викладення матеріалу, у 60-х і 70-х роках написав ще два твори, в яких з метою популяризації своїх ідей вже майже не застосовував формули. Але й ці видання за життя автора не отримали належної оцінки. «Скромный и бескорыстный труженик, – як влучно зазначив один з його біографів, – его ценность несомненно была больше, чем его известность» (Цит. за: Четвериков Н. С. Ог. Курно и его вклад в теорию вероятностей. – С. 342). Праця Курно вийшла у той час, коли у Європі панувала англійська класична школа. Проте наприкінці ХІХ та на початку ХХ століття у роботах відомих економістів та істориків вже можна було прочитати:
(Юровский Л. Н. Очерки по теории цены / Л. Н. Юровский. – Саратов, 1919. – C. 114).
Маршалл також писав, що французька школа «в лице Курно … имела конструктивного мыслителя высочайшего ранга…» (Маршалл А. Основы экономической науки / Альфред Маршалл ; [предисл. Дж. М. Кейнса ; пер. с англ. В. И. Бомкина, В. Т. Рысина, Р. И. Столпера ; под науч. ред. П. Н. Клюкина]. – Москва : ЭКСМО, 2008. – С. 718).
Поява економічного твору у відомого математика була дещо несподіваною як для сучасників Курно, так і для істориків. «Для биографов представляет своего рода загадку, каким образом среди этих многообразных трудов и, по внешней видимости, совершенно неожиданно появилось на свет экономическое сочинение Курно. Не обнаружено никаких признаков того, что до этого он проявлял интерес к политической экономии. Надо, однако, иметь в виду, что Курно был человеком энциклопедического ума и широких интересов. Очевидно, в круг его чтения входили весьма популярные в то время труды Сэя. Возможно, через Сэя он ознакомился с произведениями Смита и Рикардо. К этому надо прибавить здравый смысл и своего рода экономическую интуицию, которые очень ощущаются в книге Курно. Неудовлетворенный неточностью, зыбкостью, бездоказательностью положений экономической науки, он попытался применить к ней строгую логику и математические методы» (Аникин А. В. Юность науки : Жизнь и идей мыслителей-экономистов до Маркса / А. В. Аникин. – 4-е изд. – Москва : Политиздат, 1985. – C. 293–294).
Безперечно, головною заслугою Курно є його новаторський метод, який він запровадив у дослідженнях економічних явищ. Пояснюючи мету, яку він прагнув досягти при роботі над своїм твором, Курно писав: «…название этого труда говорит не только о теоретических исследованиях, но также о том, что я хочу к ним приложить математические символы и формулы математического анализа: вот, признаюсь, тот план, который должен привлечь ко мне осуждение чистых теоретиков…
Есть авторы, такие, как Смит и Сэй, которые написали свои работы по политической экономии в своем стиле, приводя все аргументы чисто в литературной форме, но есть и другие, как Рикардо, который, рассмотрев более абстрактные вопросы и проявив в исследованиях большую точность, не смог избежать алгебры, и только и делал, что вставлял между математическими вычислениями утомительные пояснения.
В этой работе я хочу показать, что решение общих вопросов, которые решает теория богатств, зависит, главным образом, не от элементарной алгебры, но от той отрасли анализа, которая имеет целью произвольные функции, подчиненные только некоторым условиям.
Я не хотел проводить исследования догматично, опираясь только на политическую экономию; я исключил те вопросы, где не может быть применен математический анализ, а также те, которые, как мне кажется, уже вполне разъяснены» (Курно А. О. Исследования математических принципов теории богатства / Антуан Огюстен Курно // Мировая экономическая мысль. Сквозь призму веков : в 5 т. / Моск. гос. ун-т им. М. В. Ломоносова ; [сопред. редкол. Г. Г. Фетисов, А. Г. Худокормов]. – Москва : Мысль, 2005. – Т. 2. – С. 74–75).
Політична економія, на думку Курно, займається аналізом багатства, яке він визначає як сукупність мінових цінностей. Він зосереджує увагу на об’єктивній категорії мінової цінності, яку він намагається звільнити від впливу суб’єктивних моментів – корисності, рідкості і усіх тих елементів, які є першорядними для теоретиків граничної корисності. Курно у своїх дослідженнях намагався економічні закони пояснити за допомогою математичних формул. «Курно занимает особое место в математической школе. Он впервые дал развернутое применение математического метода. Правда, и до него математический метод получал применение в экономических науках, но преимущественно как метод иллюстрации отдельных экономических положений. Курно же оперирует этим методом как методом исследования. Все отдельные положения его теории укладываются в математические формулы, причем последние у него выстроены в виде непрерывной цепи. С первого взгляда получается весьма импонирующее впечатление от экономической теории, которая по методам своего построения приближается к Евклидовой геометрии» (Блюмин И. Г. Теория Курно // И. Г. Блюмин // Критика буржуазной политической экономии / И. Г. Блюмин ; АН СССР, Ин-т мировой экономики и междунар. отношений. – Москва : Изд-во АН СССР, 1962. – Т. 1. – С. 491). Так, наприклад, Курно, розглядаючи закон вартості, пише, що є «…очень простое средство математического выражения изменений в стоимости, относящейся к товарам. Достаточно задумать систему, образованную такими же точками, расположенными по прямой линии, как имеется ряд продуктов, которые надо сравнивать так, чтобы расстояния одной из этих точек по отношению к любым другим оставались всегда пропорциональными логарифмам чисел, которые измеряют стоимость всех этих продуктов по отношению к одному из них. Все изменения расстояния, которые будут возникать из прибавления или вычитания, в силу относительных и абсолютных изменений подобной системы подвижных точек, будут вполне соответствовать изменениям их умножения и деления в сравниваемой системе значений. Отсюда следует, что чистые расчеты, определяющие наиболее вероятную гипотезу абсолютного изменения системы точек, применяются подсчетом логарифмов чисел при определении наиболее вероятной гипотезы абсолютных изменений системы значений» (Курно А. О. Исследования математических принципов теории богатства. – С. 81).
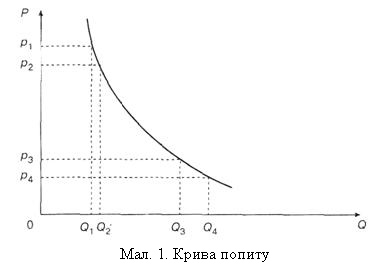
Курно вперше в економічній науці провів дослідження по визначенню рівноважного значення ціни й об'єму випуску при різних ринкових структурах – чистій монополії, дуополії, а також конкуренції з обмеженою і необмеженою кількістю господарюючих суб'єктів. Розглядаючи питання про співвідношення попиту і ціни, він також вперше застосував поняття функції попиту. Позначивши попит через Q, а ціну через р, Курно записав функцію попиту у вигляді Q = ƒ(р). Залежність між змінними була зворотна – при підвищенні ціни даного товару попит на нього зменшується, при зниженні ціни попит збільшується. Окрім цього Курно відзначив, що для різних товарів ця залежність різна і запропонував термін «еластичність попиту». Він наголошував, що попит може значно мінятися при відносно невеликій зміні цін, – це випадок високої еластичності попиту. І навпаки, попит може мало реагувати на зміну ціни – це випадок низької еластичності попиту.
Набагато випереджаючи свій час, Курно ввів «…одно из важнейших понятий современной экономической науки:
кривая спроса. Понятно, что, чем выше цена, тем меньше спрос, и наоборот. Сказанное правило принято называть
законом постепенного убывания спроса…
Кривая спроса показывает, какое количество данного товара согласны купить покупатели при различных ценах, но при данном рыночном предложении, данных доходах потребителей и т.д.» (Майбурд Е. М. Введение в историю экономической мысли : От пророков до профессоров / Е. М. Майбурд. – 2-е изд., испр. и доп. – Москва : Дело, 2000. – C. 355–356).
Ця функція безперервна. Тому її можна диференціювати, а це дало можливість Курно застосовувати диференційне та інтегральне числення до аналізу попиту. «Совокупный доход продавца (Курно обозначает его R) будет равен произведению проданного количества товаров и их отпускной цены. Поэтому, если Q = ƒ(p) есть функция спроса, то функция совокупного дохода R = pƒ(p). Далее Курно вводит еще функцию предельного дохода, а также функции совокупных издержек и предельных издержек.
В итоге получается функция совокупной прибыли:
Π=pƒ(p)–ɸ(Q),
где ɸ — функция совокупных издержек. Все эти функции, приводимые здесь в общем виде, Курно представляет аналитически, так что ими можно оперировать по правилам математического анализа.
Что нужно для отыскания максимума функции? Правильно, взять от нее первую производную и приравнять к нулю. А как убедиться, что это именно максимум, а не минимум? Опять правильно: взять вторую производную и убедиться, что в точке экстремума она отрицательна. Все это Курно и проделывает, доказывая еще при этом, что данный максимум – единственный.
Результат выходит следующим: максимум прибыли монополиста достигается при таком объеме продукции, когда предельные издержки равны предельному доходу» (Майбурд Е. М. Введение в историю экономической мысли. – C. 356).
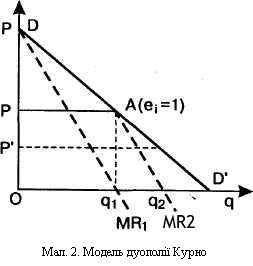
Наступним кроком у дослідженнях Курно є розгляд моделі дуополії, коли на ринку діють тільки дві фірми, кожна з яких приймає ціну і об'єм виробництва конкурента незмінними, а потім ухвалює своє рішення. При цьому кожен з двох продавців допускає, що його конкурент завжди утримуватиме свій випуск продукції стабільним. У моделі передбачається, що продавці не дізнаються про свої помилки. Фактично ж ці припущення продавців про реакцію конкурента, очевидно, зміняться, коли вони дізнаються про свої попередні помилки.
Першим починає виробництво дуополіст 1, який спочатку діє як монополіст. Об’єм виробництва його продукції складає q1, що при ціні Р дозволяє йому отримувати максимальний прибуток. При даному об'ємі виробництва еластичність ринкового попиту рівна одиниці, а загальна виручка досягне максимуму. Потім виробництво починає дуополіст 2. В його уявленні показник об'єму випуску продукції зрушиться вправо на величину Oq1 і об’єднається з лінією Aq1. Сегмент AD' кривої ринкового попиту DD' він сприймає як криву залишкового попиту, якій відповідає крива його граничної виручки MR2. Об’єм виробництва продукції дуополіста 2 буде рівний половині незадоволеного дуополістом 1 попиту, тобто сегменту q1D', а величина виробленої продукції рівна q1q2, що дасть можливість отримати максимум прибутку. Даний обсяг виробництва складе чверть всього ринкового об'єму попиту при нульовій ціні – OD'(1/2 × 1/2 = 1/4).
На другому етапі дуополіст 1, припускаючи, що обсяг виробництва дуополіста 2 збережеться стабільним, вирішить заповнити своєю продукцією вільну половину ринку, обумовлену попитом. Виходячи з того, що дуополіст 2 задовольняє чверть ринкового попиту, виробництво продукції дуополіста 1 на другому етапі складе (1/2) × (1-1/4), тобто 3/8 всього ринкового попиту, і так далі. З кожним подальшим кроком об’єми виробництва продукції дуополіста 1 зменшуватимуться, тоді як об’єми виробництва продукції дуополіста 2 збільшуватимуться. Такий процес закінчиться урівноваженням обсягів виробництва, і тоді дуополія досягне стану рівноваги Курно.
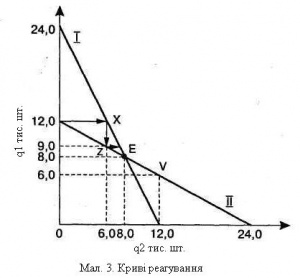
Досягнення рівноваги у моделі Курно можна зобразити через криві реагування, які відображатимуть об'єми виробництва продукції фірми, що максимізуватиме прибуток, якщо відомі дані про об'єми виробництва продукції конкурента.
На мал. 3 крива реагування I показує об'єм виробництва продукції першої фірми, що максимізувала прибуток як функцію від об'єму виробництва продукції другої фірми. Крива реагування II показує об'єм виробництва продукції другої фірми як функцію від об'єму виробництва продукції першої фірми.
Криві реагування можна використовувати для того, щоб показати, як встановлюється рівновага. Якщо рухатися по стрілкам, що намальовані від однієї кривої до іншої, починаючи з обсягу виробництва продукції q1 = 12 000, це призведе до досягнення рівноваги Курно в точці Е. При цьому кожна фірма буде випускати 8000 виробів. У точці Е перетнуться дві криві реагування. Цей випадок у економіко-математичному моделюванні дістав назву «рівновага Курно».
Модель рівноваги Курно припускає, що фірми-дуополісти конкурують одна з одною.
Ситуація принципово зміниться, якщо дуополісти досягнуть угоди і разом визначатимуть об'єм виробництва так, щоб максимізувати сукупний прибуток, а потім розділять його навпіл. Тоді на контрактну лінію припаде безліч можливих рішень.
Та якщо вони ділитимуть прибуток навпіл, то і вироблятимуть кожен свою половину продукції. Своїми розрахунками Курно доводив, що при рівновазі загальний об'єм виробництва вищий, ніж при дуополістичній домовленості, але нижчий, ніж він міг би бути при конкурентній рівновазі.
У своїх дослідженнях Курно поступово переходить і до більш складних випадків, вводячи додаткові чинники (витрати виробництва, конкуренцію, податки та інші змінні).
У результаті «Курно не лише створив теорію чистої монополії і теорію дуополії, а й висловив ідею про те, що досконала конкуренція – це граничний випадок з цілого спектра ринкових структур, визначених кількістю продавців. Він показав, що дуополісти врешті-решт дійдуть до спільної ціни на мінеральну воду, нижчої від монопольної, але вищої за ціну, породжену вільною конкуренцією багатьох продавців; так само монополія виробляє найменший обсяг продукції, а конкуренція – найбільший, так що випадок дуополії опиняється між їхніми межами. Він дотримувався цікавої думки, що однорідна продукція будь-якої сукупності n фірм дорівнює n/(n+1) помноженому на продукцію конкурентної галузі: із збільшенням кількості фірм обсяг виробництва галузі прямує в границі до обсягу виробництва досконало конкурентної галузі. Тут у зародку міститься популярне потім уявлення про досконалу конкуренцію як мірило для оцінювання результатів функціонування неконкурентних ринкових структур» (Блауг М. Економічна теорія в ретроспективі : пер. з англ. / М. Блауг. – Київ : Вид-во Соломії Павличко «Основи», 2001. – C. 292).
На початку ХХ сторіччя багато економістів називали модель Курно наївною, що не враховує багатьох важливих економічних факторів виробництва. Так, російський економіст В. К. Дмитрієв, провівши свої розрахунки, дійшов висновку про те, що «…несмотря на то, что в каждый данный момент, для которого произведенное количество является величиной постоянной, размер предложения и цена будут определяться совершенно одинаково как для обладателя-монополиста, так и для конкурирующих предпринимателей, – самый размер производства определится в этих случаях совершенно различно: в то время как монополист-производитель остановится на величине производства, равной общему предложению, дающему наибольший общий доход, – конкурирующие производители в погоне за «мгновенной выгодой» будут безгранично увеличивать каждый свое производство, а вместе с тем и общее производство. Как видим, этот результат отличается от вывода Курно, который утверждал, что размер, до которого n предпринимателей расширяет общее производство,
будет равен D из уравнения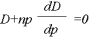 
и, следовательно, будет равняться величине бесконечно большей лишь при n =∞» (Дмитриев В. К. Экономические очерки / В. К. Дмитриев. – Москва : Высш. шк. экономики, 2001. – С. 160–161).
Проте всі покоління економістів пам’ятатимуть, що талановитий вчений запропонував перш за все «новий інструмент» для досліджень. «Математик по образованию, – зазначає М. С. Четверіков, – он в своем творчестве вышел далеко за пределы чистой математики. В экономической науке он явился по существу первым экономистом-математиком. … он заложил основы современной математической экономии, применил методы математического анализа к исследованию экономических явлений и процессов, измеряемых количественно. И хотя до Курно многие авторы пытались применить математические приемы к политической экономии, однако только Курно первому, по справедливому замечанию Ирвинга Фишера, удалось достичь в этом направлении значительных результатов» (Четвериков Н. С. Ог. Курно и его вклад в теорию вероятностей. – С. 341). В історії економічної науки Курно назавжди залишився першим «…автором, который дал определение функции спроса и начертил ее график, а также первым, кто всерьез применил в экономике дифференциальное исчисление для решения задачи на нахождение максимума» (Блауг М. 100 великих экономистов до Кейнса / М. Блауг ; пер. с англ. под ред. А. А. Фофонова. – Санкт-Петербург : Экон. школа, 2005. – С. 152).
